2012 April

Continued from: Part 2 – Enumerate Ranges and First/Last

This is really the major piece of work in this release. There are a number of factors as to why these methods were added, but the foremost among them is performance when merging two sets of data. Before we go further let’s look at a typical scenario where we just fetched 1000 records from the server and need to insert them into our local cache. For this example let’s assume our records are 256 bytes, giving us a b+tree order of 32 values per leaf to fill 8kb blocks. This data is key’ed by it’s parent ID + name so the key space we are going to write is very dense. The thing I started to wonder is how much wasted thrashing is going on while enumerating and inserting densely populated keys. Basically we go find a node, rewrite that node, get the next item, find the same node we just had, rewrite it again, and so on. Let’s do a little math and find out how bad is this?

So how many read/write operations are there inserting these 1000 nodes one at a time (btree order 32)?

Would you believe around 1200! It should be obvious it’s over 1000, where are the other 200+ coming from? Splits. Each time we need to insert into a full node we have to split it, that requires rewriting that node, it’s parent, and it’s new sibling. This means that our 68 node tree has written 3×68 times just in splits.

AddRange

So what if we could fill a node before writing it the first time?

Obviously this requires a precondition, the input must be sorted. Once that precondition is met though we can now insert the entire set just as before except we will completely fill a node prior to writing it (if possible). Of course not every key can be placed in any node, thus to gain from this not only will the input need to be sorted, but the keys need to be dense enough that the optimization will help. As an example inserting 100 random GUIDs into a btree of 100,000 GUIDs will not likely see any gain whereas inserting 100 random GUIDs into a btree with 100 items will.

So how many read/write operations are there using this method on these 1000 pre-ordered nodes (btree order 32)?

Only 270+ since that is the same 200+ splits with the addition of another write for each of the 63 leaf nodes. We just gained nearly an order of magnitude. Thus the AddRange methods where born. They use these mechanics and typically see a 5 to 10x improved speed for the insert.

BulkInsert

But wait, we can do better! What if we did not need to split the nodes during write, can we just fill and move on and write in O(n) time? I mean if we can write all 68 nodes once that’s a far sight better than 270+ writes, further we can even reduce the number of nodes needed by leaving them all full.

So how many read/write operations are there using this method on these 1000 pre-ordered nodes (btree order 32)?

Just 33 (assuming it’s currently empty). That means we gain another order of magnitude over AddRange, but what about the existing contents? Well it needs to be entirely read and rewritten back to disk for this to work, and again our input needs to be sorted. Luckily our existing content is already sorted so we can merge it with the input in O(n) time, that is the easy part. There is some added overhead since we will need to rewrite the root and delete all the ‘old’ data, but it’s still O(n) insertion time, where n is the number of items in the b+tree plus the number being inserted.

The other nice thing about this approach is that by rewriting the tree we can use a transaction to swap the root node. This allows an all-or-nothing insert that was previously not possible. In future versions this may be used for replacing or removing ranges of data.

Confirming our Performance SWAG

The following graph displays the same data inserted via the various options above:

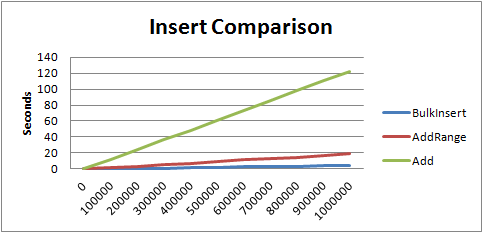
I’m pleased to see the chart so clearly back up the math. The order of magnitude between variations is not just theory any more ;) The insertion times graphed above are 3 seconds for BulkInsert, 18 seconds for AddRange, and 122 for Add.
*Note: in the real-world case of sparse key inserted to existing data the results will vary widely.

BulkInsert a Billion Rows…

Sure we can do that in under an hour :)

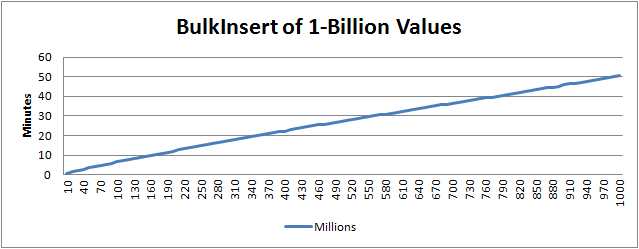
Why would you insert a billion rows? Just because we can. Does anyone know how long inserting a billion rows into SQL Server with Bulk Import takes?

Update: The preceding times were measured with the original file format. The v2 format is much faster that represented here. Additionally I’ve tested up to Int32.MaxValue (2,147,483,647) rows with no issues and linear performance. Keep reading the following articles for more information on the v2 storage format.

Presorting Input

Given the above methods both depend upon presorted data we need to address this. The only complication is that we could be inserting more data than can reasonable be placed in memory. Enter the OrderedEnumeration<T> class. This class takes an enumeration, breaks it into ‘pages’ of data that can fit in memory, sorts it, and if needed stores the result on disk. Finally the class then aggregates all pages into a single ordered enumeration. The whole thing is done in O(n log(n)) time, and given that the disk access is sequential, this can be done much faster than directly inserting the data. I stopped testing at 100 million rows and found no measurable difference between presorted and unsorted input.

Usage Notes:

AddRange will always sort the data. Use AddRangeSorted if the data is already sorted by key. AddRange may also be used to overwrite existing data by providing true for the optional argument ‘allowUpdates’. AddRange is thread-safe and allows concurrent writers to exist in the tree.

AddRangeSorted will assume the input enumeration is already ordered. If the data is out of order, no harm will come; however, it may be no more optimal than just calling Add() for each item. AddRangeSorted is thread-safe and allows concurrent writers to exist in the tree.

BulkInsert will by default sort the input enumeration. Use the overload that accepts a BulkInsertOptions structure to specify the input as presorted if needed. Warning: if the input is not actually sorted and the options provided declare it as being sorted, the resulting structure will be corrupt (or an exception may be thrown). BulkInsert is thread-safe and is a write exclusive operation on the tree; however, it does allow concurrent readers to still read the previous state while the tree is being rewritten. BulkInsert is also a transacted operation, either all records will be added/updated or none but no incomplete results are possible.

Next up BPlusTree 2.0 Changes Part 4 – Rewriting the Storage Format

Continued from: Part 1 – Interface Changes

Enumerating Ranges
I’ve been contacted several times about adding the ability to enumerate ranges from the b+tree. It’s actually a very trivial thing to implement and I’ve handed out the code several times. With this release the following range enumeration methods will be available:

EnumerateFrom(TKey start) – Enumerate from (inclusively) the specified key.
EnumerateRange(TKey start, TKey end) – Enumerate from (inclusively) the start key until the next key follows the end key.

Example:

    var options = new BPlusTreeOptions<char, string>(PrimitiveSerializer.Char, PrimitiveSerializer.String);
    using(BPlusTree<char, string> btree = new BPlusTree<char,string>(options))
    {
        btree.AddRange(
            "qwertyuiopasdfghjklzxcvbnm"
            .ToCharArray()
            .Select(c => new KeyValuePair<char, string>(c, new String(c, 1)))
        );
        Assert.AreEqual(
            "jklmnop",
            new String(btree.EnumerateRange('j', 'p').Select(kv => kv.Key).ToArray())
        );
    }

Keys and Values Collections
The previous implementations of the properties Keys and Values have been re-implemented. They were doing a complete enumeration each time they where accessed. Now there is an actual class behind these that simply wraps the existing class-level enumeration. There is not, as yet, a means to enumerate only the keys or values from a range. Since there is not a performance benefit users should just use Linq’s .Select() extension to extract the key or value from the KeyValuePair as shown above.

First, Last, and TryGetFirst/Last
One project I was working with needed to be able to find the last key used in the dictionary so I could retrieve it’s value. Previously this meant you had to enumerate the entire dictionary. With ranged enumeration you might even been able to enumerate a small portion, but that is still a waste. The First() and Last() methods will now efficiently retrieve the key/value pairs for you. If there is a risk the dictionary is empty you can use the TryGetFirst() and TryGetLast() methods. These methods allow using the b+tree as a disk-based work queue of sorts (which is what I was doing, using a key-structure that sorts by priority, time, and then Guid).

Please note that the First() and Last() methods will throw InvalidOperationException if the collection is empty.

Let’s move on to bigger and better things…
Continue reading: Part 3 – AddRange and BulkInsert

After much deliberation on the subject, I decided to introduce breaking changes interface. I know, I know, I don’t do this lightly, in fact I think it’s the third worse thing I could possible do (sorry it does follow adding bugs and semantic changes). So here are my reasons why I thought this was necessary:

Calling Add() was habitual and was seldom, if ever, checking the return value for errors or key collisions.
The return value of Add() reflected two possible states, failure or a key collision, with no way to differentiate between them.
The delegate used in the atomic update method did not provide the key, so every time I used it I had to define an anonymous method to inject the key I was updating.
The boolean return value of Update again signaled numerous possible outcomes, either the key was not found, it failed, or the resulting value was equal to the existing value.
Lastly, I found and reviewed the ConcurrentDictionary interface and found it exactly matched my needs.

So as much as I hate to do so, I am breaking the interface. I wouldn’t do so if I didn’t wholeheartedly believe that we will both be better off for it. If you have an existing project the conversion is trivial, just insert “Try” after the ‘.’ for all the errors and you’ll be mostly there. If you want to stick to the version you have that should be viable, I’ve made no bug fixes as I haven’t found any. So the following methods have been added, most of these taken from the ConcurrentDictionary:

    void Add(TKey key, TValue value);
    bool TryAdd(TKey key, Converter<TKey, TValue> fnCreate);
    bool TryAdd(TKey key, TValue value);

    TValue GetOrAdd(TKey key, TValue value);
    TValue GetOrAdd(TKey key, Converter<TKey, TValue> fnCreate);

    TValue AddOrUpdate(TKey key, TValue addValue, KeyValueUpdate<TKey, TValue> fnUpdate);
    TValue AddOrUpdate(TKey key, Converter<TKey, TValue> fnCreate, KeyValueUpdate<TKey, TValue> fnUpdate);
    bool AddOrUpdate<T>(TKey key, ref T createOrUpdateValue) where T : ICreateOrUpdateValue<TKey, TValue>;

    bool TryUpdate(TKey key, TValue value);
    bool TryUpdate(TKey key, TValue value, TValue comparisonValue);
    bool TryUpdate(TKey key, KeyValueUpdate<TKey, TValue> fnUpdate);

    bool Remove(TKey key);
    bool TryRemove(TKey key, out TValue value);
    bool TryRemove(TKey key, KeyValuePredicate<TKey, TValue> fnCondition);
    bool TryRemove<T>(TKey key, ref T removeValue) where T : IRemoveValue<TKey, TValue>;

Sorry again for any inconvenience, yet I think you will agree that the final interface is much cleaner and clearer. The following outlines the intended behavior of these methods:

All methods now throw on internal failures to avoid ambiguous return values.
Boolean methods do not return false when the updated value equals the existing value.

Continue reading: Part 2 – Enumerate Ranges and First/Last

I’ve recently seen some comments about various aspects of btree/b+tree structures that are troublesome. They are, IMHO, just plain wrong. Let’s look at a few of these and see if we can shed some light on b+trees and their implementations.

1. Items in a tree node must be presorted.
FALSE This is simply not true, a btree can decide to sort the items in a node, or to perform a linear search. Neither approach change more than the small constants in the big-O, it’s still O(n log(n)). The BPlusTree keeps it’s children sorted since the memory-move cost is nothing compared to the disk IO.

2. Split/Join of a node requires reorganizing it’s ancestors
FALSE While this is the most common approach it is also the most naive. Reorganization of the tree from the bottom-up is not only expensive but more complicated than the top-down approach. The BPlusTree uses a top-down reorg that says simply “If I’m inserting and this node is full, split” all the way down the tree. This means that at any given time I only need two nodes ‘locked’ for write, me and my parent. Once I’m sure that this node is not full I can release my parent’s lock and move down the tree. Not only does this strategy allow multiple concurrent writers, but it also prevents deadlocks. By using this top-down approach locks are always acquired at the root and traverse down so that a deadlock is simply impossible.

3. Nodes can have at most order-1 items
FALSE This is also a naive implementation detail where leaf nodes (or all nodes) have a vacant slot. It’s most commonly used when using a bottom-up reorganization so that you always have room to insert a split node. It is simply not necessary with either bottom-up or top-down reorganization, it’s just easier. BPlusTree uses all the space available in a node, only when inserting and already full will it split the node.

4. Nodes can have no fewer than order/2 items
FALSE The minimum items in a node is 1. When you calculate the lookup time with a minimum of 1 (let b = 1) you get O(log_bn) or O(n). So you never want a minimum value of 1, but you can do it. Based on my own testing the best value for the minimum node count in BPlusTree is 1/3 of the order (or max).

5. The order of a btree is the same at all levels
FALSE The BPlusTree supports having a different order for hierarchy nodes than that of it’s leaf nodes. The reason is simple. Disk-based B+Trees optimize disk access based on what will fit in a ‘page’. Using 8kb as a page size, at the leaf node this is 8192 / (sizeof(key) + sizeof(value)). At all other locations in the hierarchy this is 8192 / (sizeof(key) + c) where c is some constant size of data used to reference a child node. This means that if I am storing 1kb records with a 4-byte key I want no more than 8 records in a leaf, whereas I can have as many as 680 children in a non-leaf node. Now we can let b = 680 for O(log_bn), meaning we can find the leaf node of a 1,000,000 item tree in approximately 3 operations.

csharptest.net

BPlusTree 2.0 Changes Part 3 – AddRange and BulkInsert

AddRange

BulkInsert

Confirming our Performance SWAG

BulkInsert a Billion Rows…

Presorting Input

Usage Notes:

BPlusTree 2.0 Changes Part 2 – Enumerate Ranges and First/Last

BPlusTree 2.0 Changes Part 1 – Interface Changes

Dispelling Myths about B+Trees

Search

Projects

Recent Updates